Bearbeiter:
Arne Sendke
Carl Goos
Dirk Rose
Die Stundenplanung des Gymnasiums ist z.Zt. ein fast einwöchiger Vorgang, in dessen Verlauf mit Hilfe einer EDV-Anlage eine zulässige Basislösung generiert wird, welche allerdings nicht die Präferenzen der Schüler und Lehrer berücksichtigt. Um also diese Lösung weiter zu verbessern, werden an einer riesigen Stecktafel per "Trial-and-Error" alternative Stundenpläne erarbeitet. Dies ist sehr langwierig und führt nicht zwangsläufig zur optimalen Lösung, sondern wird beendet, sobald der Plan für alle Entscheidungsträger akzeptabel ist.
Aufgabe ist es nun, diese Stundenplanung vom improvisierten zum durchstrukturierten Vorgang weiter zu entwickeln und die für die einzelnen Teilbereich notwendigen Berechnungen in einem Modell zusammenzufassen und mit Hilfe einer Modellierungssprache abzubilden. Hierzu sind zunächst die einzelnen Bereich abzugrenzen, die entsprechenden Daten zu erheben und die für den Entscheidungsprozeß relevanten Daten festzulegen.
Durch einen Besuch vor Ort wurden die Daten für die Oberstufe erhoben und es konnten die für den Stundenplan unbedingt einzuhaltenden und darüber hinaus wünschenswerten Eigenschaften festgestellt werden.
Nach ergebnisloser Bibliotheks- und Internetrecherche, in der es uns nicht gelang, weiterreichendes Material zu finden, erhielten wir einen Artikel von Jan Stallaert in die Hände, in welchem er die Stundenplanung an amerikanischen Universitäten thematisierte. Leider waren die dort vorgestellten Ansätze nicht auf unserer Problem übertragbar, da viele Voraussetzungen gemacht wurden, welche für das zu bearbeitende Problem nicht zulässig waren. Desweiteren wurde in der Abhandlung bemerkt, dass das Problem zu komplex ist, um optimal gelöst zu werden und außerdem keine wissenschaftliche Ansätze zu diesem Problem existieren.
In der Fachzeitschrift "Spektrum der Wissenschaft", Ausgabe 2/99, wurden neue Lösungsmethoden thematisiert. Hierbei wurde auch das Stundenplanproblem angesprochen. Geschrieben ist der Artikel von Prof. Dueck , Mitarbeiter des wissenschaftlichen Zentrums von IBM in Heidelberg, IEEE Fellow und erhielt 1991 den IEEE Prize Paper Award der Information Theory Society und Professor Scheuer, Mitarbeiter SAP in Walldorf in der Entwicklung des Systems APO (Advanced Planer and Optimizer). Aus diesem Artikel hierzu ein Auszug:
" Eine weitere große Klasse von Optimierungsaufgaben behandelt Pläne für Zeitabläufe. Am bekanntesten ist das Erstellen eines Stundenplans für die Schule. Es ist schon sehr schwer, überhaupt eien Lösung zu finden, die zulässig ist. Lehrerdeputate, Oberstufenkursblöcke und Fachräume müssen beachtet werden. Wenn der Planer lange gearbeitet hat und fast fertig ist, entdeckt er typischerweise, daß Klasse 6b eine Stunde zu wenig Sport hat. Zu den noch verfügbaren Zeiten ist jedoch die Turnhalle belegt Läßt sich nach einigem Hin und Her doch ein Termin finden, gibt der Sportlehrer in dieser Stunde gerade Englisch in der 11a. Dieses Problem ist so schwierig, daß in aller Regel der zum Unterrichtsbeginn erreichte Stand der Überlegungen wohl oder übel als Stundenplan für ein ganzes Halbjahr herhalten muß.
Ein Plan, so man ihn denn hat, ist gemeinhin sehr sensibel gegen Änderungen. Fällt zum Beispiel eine Lehrerin wegen Mutterschaftsurlaubs aus, muß meist ein großer Teil des Plans umgestoßen werden."
Dieser Auszug veranschaulicht sehr gut die Problematik des Stundenplanens. Auch hier wird angedeutet, daß es schon ein Problem ist, überhaupt eine Lösung zu finden.
Dieser Teil unserer Abhandlung beschreibt zunächst textuell die Vorgehensweise bei der Modellierung des Problems und die einzelnen betrachteten Teilbereiche. Im Anschluß finden sich dann die Formeln und AMPL-Programme, welche wir für die Modelle eingeführt haben.
Gelenkt durch den Mangel an Fachliteratur und in Kenntnis um die Komplexität des Problems, wurden, um das Problem handhabbar zu machen, einige Vorgaben (Sonderregelungen etc.) in die Lösung zunächst nicht mit einbezogen. Außerdem besteht der Ansatz nicht aus einem großen Modell, sondern aus ineinander verzahnten Teilmodellen.
Während des Projektes entstand ein weiterer Lösungsansatz, der aufgrund des späten Zeitpunkts nur skizziert wurde. Dieser wird am Ende dieses Berichtes erläutert.

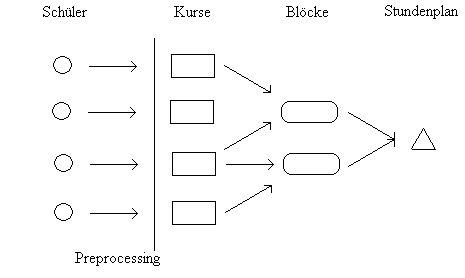
Auf Basis der von der Schulleitung vorgegebenen Wahlmöglichkeiten hat jeder Schüler für das betrachtete Halbjahr eine Menge von Kursen belegt. Ausgehend von dieser Datenmenge kann nun ohne ein kompliziertes Optimierungsmodell errechnet werden, welche Kurse stattfinden, welche aufgrund von Unterbelegung ausfallen müssen, und von welchem Kurs sogar zwei oder mehr angeboten werden müssen. Als Berechnungsgrundlage dient auch hier die Vorgabe der Schulleitung, dass ein Kurs mindestens 10, höchstens 29 und im Schnitt 19,5 Schüler aufnimmt. Als Ergebnis dieser Vorberechnung erhält man für die weiteren Optimierungsmodelle eine Menge von zu betrachtenden Kursen, welche dort als Inputdatensatz dient.
Dieses Teilmodell ist das komplizierteste, da es einen Großteil der Restriktionen beinhaltet und eine starke Verknüpfung zu den anderen Teilbereichen aufweist. Die Blockung ist notwendig, um festzulegen, welche Kurse zeitgleich stattfinden. Demnach können nur Kurse in denselben Block gelangen, welche dieselbe wöchentliche Stundenzahl haben.
Die Hauptschwierigkeit in diesem Teilmodell liegt darin, sicherzustellen, dass möglichst wenig Kurse im selben Block liegen, die ein und derselbe Schüler besuchen möchte, da diese Kurse nach Definition der Blöcke zeitgleich stattfinden. Diese Schwierigkeit ist Ausdruck des Soft Constraints "Präferenzen der Schüler", denn wenn ein Schüler einen von ihm gewählten Kurs aus zeitlichen Gründen nicht belegen kann, so wirkt sich dies sehr negativ auf seine qualitative Einschätzung der gefundenen Lösung wieder. Überschneidungen müssen also modellhaft stark "bestraft" werden.
Desweiteren müssen die Raum- und Lehrerrestriktionen beachtet werden, denn es dürfen z.B. nicht vier Sportkurse in einem Block liegen, da nur drei Sporthallen zur Verfügung stehen.
Sind die Blöcke fertig gestellt bedarf es einer Zuordnung der Blöcke in die Zeittaffel. Hierbei muß beachtet werden, dass bei zweistündigen Blöcken diese nicht zerrissen werden, also daß die beiden Stunden hintereinander liegen. Des weiteren darf diese Doppelstunde nicht über eine Pause laufen. Bei dreistündigen Kursen dürfen die drei Stunden nicht an einem Tag erfolgen.
Es folgen nun die von uns erstellten Restriktionen.
Hier wird überprüft, ob nicht zu viele Kurse, die von der gleichen Fachart sind gleichzeitig stattfinden und zu wenige Räume für diese Kursart vorhanden sind.
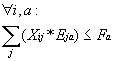
Hier wird überprüft, ob genügend Lehrer für die jeweilige Kursart innerhalb eines Blockes vorhanden sind.
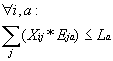
Es müssen in einem Kurs mindestens 10 und höchstens 29 Schüler sein.
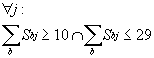
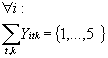
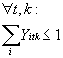
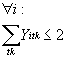
Ziel:
![]()
bzw:
Ya =>Yb und Yc (IV)
![]() sonst Ya = 0 I
sonst Ya = 0 I
![]() sonst Yb = 0 II
sonst Yb = 0 II
![]() sonst Yc = 0 III
sonst Yc = 0 III
I:
![]()
II:
![]()
III:
![]()
IV:
![]()
Die Springstundenrestriktion spielt für unseren Teilbereich ohnehin keine Rolle, da hier nur die Oberstufe betrachtet wird und für die Springstundenermittlung natürlich die Kenntnis aller Unterrichtsstunden eines Lehrers voraussetzt. Desweiteren ist der von uns entdeckte mathematische Ausdruck rekursiver Art und daher leider nicht in AMPL modellierbar. Zum Verständnis sei gesagt, dass sich die Anzahl der Springstunden wie folgt berechnet:
Von der Anzahl der maximalen Stunden pro Tage (hier 9) werden zunächst die Unterrichtsstunden des Lehrers subtrahiert, da diese auf keinen Fall Springstunden sein können. Dann stellt man fest, wie viele zusammenhängende Freistunden der Lehrer vor seiner ersten und nach seiner letzten Unterrichtsstunde hat und subtrahiert auch diese Werte. Der Rest stellt die Springstunden des Lehrers an diesem Tag dar.
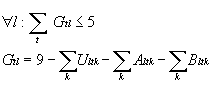
Alt1=1, falls Ult1 = 0
Alt1=0, falls Ult1 = 1
Altk= 0, falls Ultk = 1
Altk= 0, falls Ultk = 0 ![]()
Altk= 1, falls Ultk = 0 ![]()
Blt9= 0, falls Ult9=1
Blt9= 1, falls Ult9=0
Bltk= 0, falls Ultk=1
Bltk= 0, falls Ultk=0![]()
Bltk= 1, falls Ultk=0![]()
Wie bereits erwähnt, entstand gegen Ende des Projektes ein völlig neuer Lösungsansatz. Dieser entstand aufgrund der Vermutung, dass der erste Ansatz mit Hilfe von linearer Programmierung schwer umzusetzen sei. Es handelt sich aber nur um einen Ansatz.
Ausgangspunkt ist die Wahl der Schüler. Für jeden Schüler wird ein trivialer Stundenplan ermittelt. Hierbei wird nur der jeweilige Schüler betrachtet. Es fliessen in diesen Stundenplan natürlich die
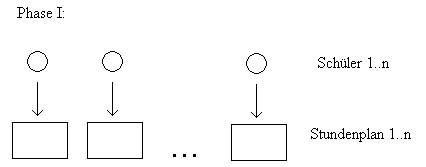
geltenden Restriktionen mit ein.
Als weiteren Schritt werden nun alle gleichen (wenn es denn welche gibt) Stundenpläne zusammengefasst. Es bleibt eine gewisse Anzahl von unterschiedlichen Stundenplänen übrig, von denen man weiß, daß diese gültig sind und alle Restriktionen erfüllen, sowie alle Schüler aufnehmen.
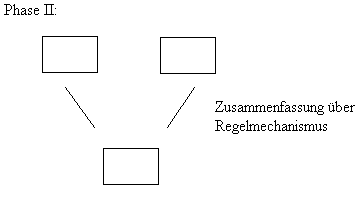
Es gilt nun, diese Pläne zu einem zusammenzufassen. Hierzu muß sich so etwas wie ein Regelwerk überlegt werden, der zwei Pläne in einen neuen überführt. Jede Überführung kann dabei nach Zielkriterien gewichtet werden.
Es sollte zum Schluß ein Plan entstehen, der sehr viele Schüler erfasst. Übriggebliebene Pläne (und somit Schüler) müssen ihre Wahl abändern, um in den Plan zu gelangen.