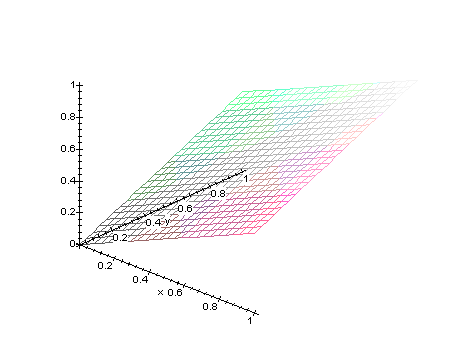
Abbildung zweier Gleichungssysteme und deren
Differenz auf 3D-Körper.
Das erste Gleichungssystem besteht aus der Ungleichung:
yb + ya – 2yc >= 0
Dieses wird für Maple durch auflösen nach yc und gleichsetzen mit x,y,z zu
z=0.5*x+0.5*y
Unter Maple wird dies repräsentiert durch den Code:
f1:=0.5*x+0.5*y;
plot3d({f1}, x=0..1, y=0..1, axes=normal);
und als 3D-Darstellung:

Die Ursprungsgleichung ist äquivalent zu dem zweiten Gleichungssystem, bestehend
aus den Gleichungen:
yb >= yc
ya >= yc
Auch dieses wird für Maple mit x,y,z gleichgesetzt und liefert somit:
x=z
y=z
Das zweite System wird in Maple wie folgt eingegeben:
f2:=x;
f3:=y;
plot3d({f2,f3}, x=0..1, y=0..1, axes=normal);
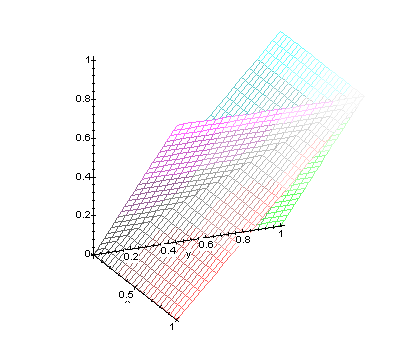
Diese Darstellungen lassen sich auch als Körper abbilden.
1. Eine Gleichung:
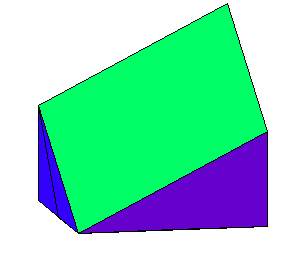
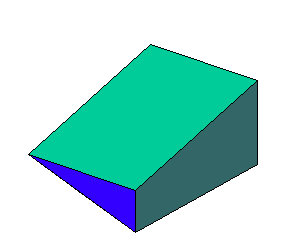
2. Zwei Gleichungen:
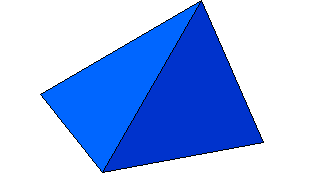

3. Die Differenz (1-2):
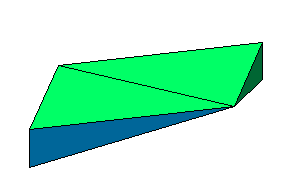
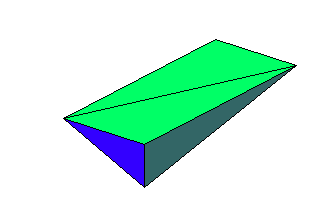
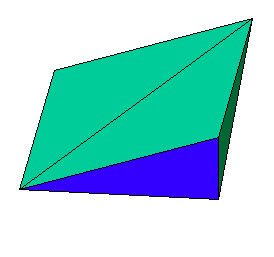
Anhang:
Maple Code:
f1:=0.5*x+0.5*y;
f1 := .5 x + .5 y
plot3d({f1}, x=0..1, y=0..1, axes=normal);
PLOT3D(POLYGONS([[2,0,0],[0,0,1],[0,2,0],[2,2,-1]],
[[2,0,0],[0,0,1],[0,0,-1],[2,0,-1]],
[[0,2,0],[0,0,1],[0,0,-1],[0,2,-1]],
[[2,0,0],[2,0,-1],[2,2,-1],[2,1,-1]],
[[0,2,-1],[0,2,0],[2,2,-1],[1,2,-1]],
[[0,0,-1],[2,0,-1],[0,2,-1],[2,2,-1]]),
LIGHT(0,0,0.0,0.7,0.0), LIGHT(100,45,0.7,0.0,0.0),
LIGHT(100,-45,0.0,0.0,0.7), AMBIENTLIGHT(0.4,0.4,0.4),
TITLE(Eine_Gleichung),STYLE(PATCH),COLOUR(ZHUE));
f2:=x;
f3:=y;
plot3d({f2,f3}, x=0..1, y=0..1, axes=normal);
PLOT3D(POLYGONS([[0,0,0],[1,0,0],[0,1,0]],
[[1,0,0],[0,1,0],[1,1,1]],
[[1,0,0],[0,0,0],[1,1,1]],
[[0,1,0],[0,0,0],[1,1,1]]),
LIGHT(0,0,0.0,0.7,0.0), LIGHT(100,45,0.7,0.0,0.0),
LIGHT(100,-45,0.0,0.0,0.7), AMBIENTLIGHT(0.4,0.4,0.4),
TITLE(Zwei_Gleichungen),STYLE(PATCH),COLOUR(ZHUE));
PLOT3D(POLYGONS([[0,0,0],[1,0,0],[1,0,0.5]],
[[1,0,0],[1,0,0.5],[1,1,1]],
[[0,0,0],[1,1,1],[1,0,0.5]],[[0,0,0],[0,1,0],[0,1,0.5]],
[[0,1,0],[0,1,0.5],[1,1,1]],
[[0,0,0],[1,1,1],[0,1,0.5]]),
LIGHT(0,0,0.0,0.7,0.0), LIGHT(100,45,0.7,0.0,0.0),
LIGHT(100,-45,0.0,0.0,0.7), AMBIENTLIGHT(0.4,0.4,0.4),
TITLE(Diferenz),STYLE(PATCH),COLOUR(ZHUE));