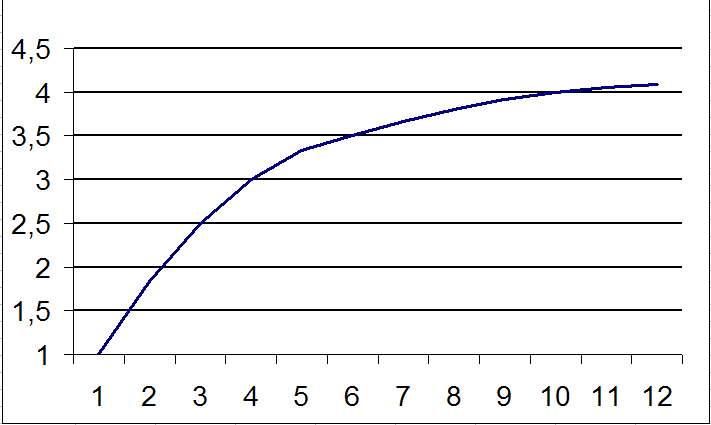
Die Wahrscheinlichkeit, Mindestwürfe (MW) bei Shadowrun zu erreichen folgen keinem linearen Verlauf. Durch den Re-Role im Falle einer Sechs ist jeder MW über 6 unlinear. Beispiel: die Wahrscheinlichkeit einen MW von 6 zu schaffen ist halb so hoch, wie die, einen MW von 5 zu schaffen, d.h. die Anzahl der Erfolge wird halbiert. Gleichzeitig gibt es keinen Unterschied zwischen einer 6 oder einer 7 als MW und es gibt nur einen Unterschied von 17% zwischen 7 und 8 (nur einer von 6 Würfeln schafft nicht die 8).
Folgende Grafiken sollen dieses Verdeutlichen:
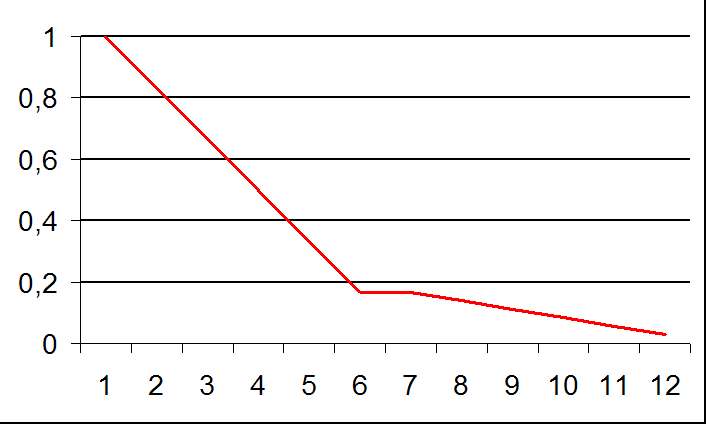
Die Betrachtung der Einzelwahrscheinlichkeiten offenbart, das diese streng linear verlaufen, mit Sprüngen an den 6er Stellen.
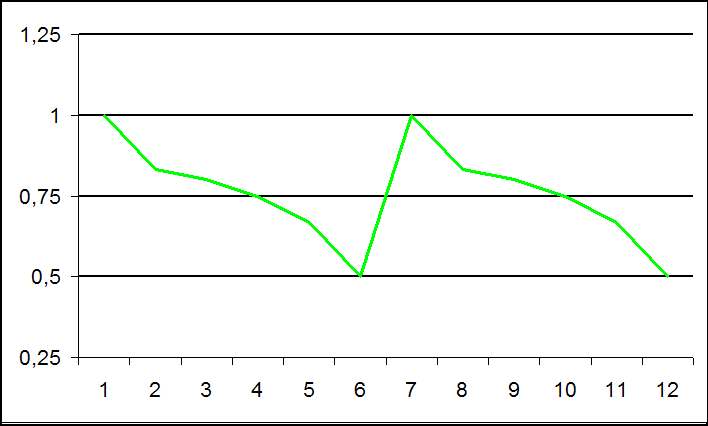
Achtet man auf die Unterschiede zwischen den Wahrscheinlichkeiten, so kommt man zu folgender Grafik, in der deutlich wird, das z.B. die # der Erfolge zwischen einem MW von 5 zu 6 halbiert wird, während die # der Erfolge zwischen 6 und 7 konstant (bei 1) bleibt. Deutlich sieht man hier den Zyklus, der sich alle 6 MW ergibt.
In der letzten Grafik wird noch einmal die Summe der Einzelwahrscheinlichkeiten dargestellt, aus der sich, im Gegensatz zu linearen Wahrscheinlichkeitsverläufen, eine abnehmende Kuve ergibt.